Gaussian Process Prior VAE for Interpretable Latent Dynamics from Pixels
The Problem
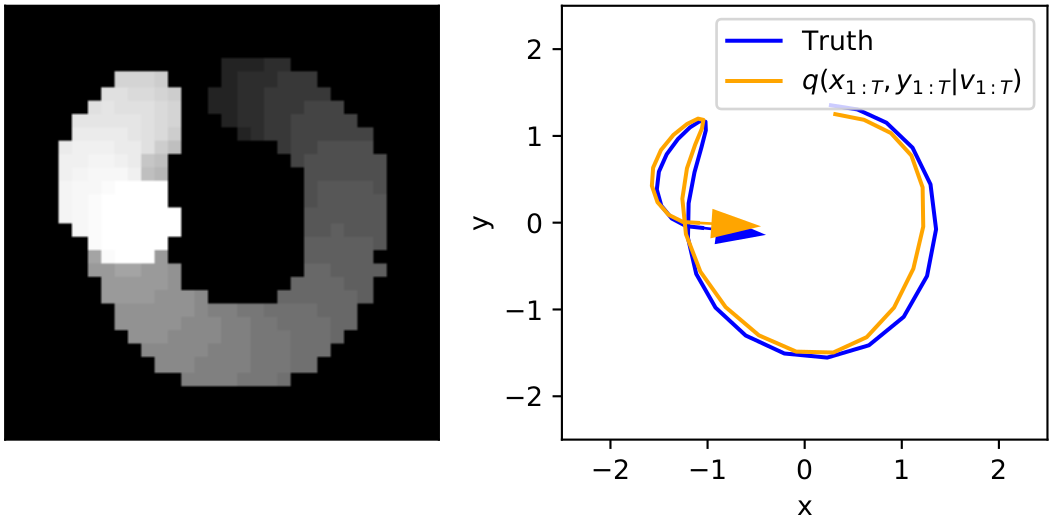
Given a set of videos that looks like this:

we know that the videos have low-dimensional structure, in this case there is only so many white pixels on screen at once, and there is also a lot of similarity between consecutive frames. Can we use this simple underlying structure and correlation-through-time to learn a physically plausible time series of \((x,y)\) coordinates?
In this work we consider doing just that, however with a few extra requirements:
-
For any frame, we could obviously just use indeces of the most top left white pixel as a prediction of \((x,y)\) location. But such a solution is unique to this dataset and won’t generalise to colorful real world video (future work).
-
For speed at test time, it must be amortised: we desire a single function that goes from videos, image time series \(v_{1:T}\), to location time series, \((x_1,y_1),...,(x_T, y_T)\). (As opposed to mean-field methods that find \((x_t,y_t)\) by an inner optimisation to match \(v_t\)).
-
It must be able to handle different length videos: 2 frames, 10 frames, 100 frames, videos vary in length.
The Solution
Previous solutions, such as the Kalman-VAE, have combined high-capacity LSTM with low capacity Kalman-filtering. This allowed interpretable physically plausible latent space but required training tricks: freeze-thaw of parameters, a handcrafted training schedule…. We skip the Kalman filter + LSTM and consider a Gaussian process. This simplifies the maths, reduces Monte-Carlo approximations, stabilises training, however, increases computional complexity.
Let’s assume that the underlying \((x,y)\) time series can be modelled by a standard Gaussian process. For simlpicity, let’s say we have 30 frames, we can take each frame, \(v_1,...,v_{30}\), use a neural network to encode it into a pair \((\mu^*_x(v_t), \mu^*_y(v_t))\in\mathbb{R}^2\).
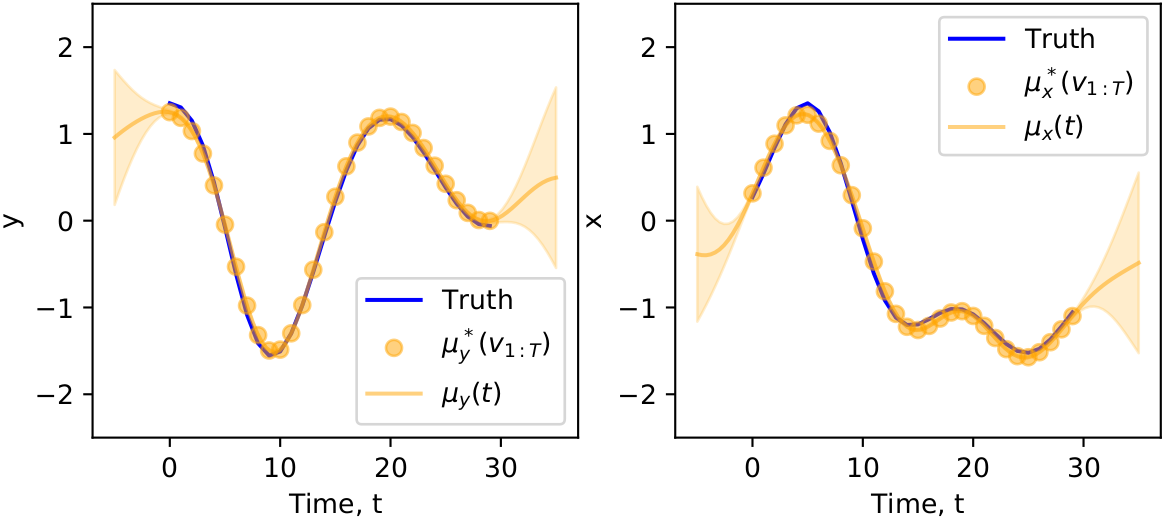
Next, take all of the \(x\) values of the encodings and their time stamps \((1,\mu_x^*(v_1)),....,(30, \mu_x^*(v_{30}))\), and simply treat them as points for standard 1D Gaussian process regression over time. This way we get a prediction with uncertainty \(x(t) \sim N( \mu_x(t), \sigma^2_x(t))\) for any time that includes information from all frames. We do the same for the \(y\) values too. Below left is a video with frames overlayed and shaded by time, right is the GP regression applied to the time series of encodings.
And the Gaussian process for each coordinate looks like
Finally, we derive the evidence lower bound and train in tensorflow shown below. Notice how to begin with, the encoded (x,y) points are rather tangled and messy, but, they get “unwrapped” and ironed out as training continues, focus on the top-right points of the circle plot,
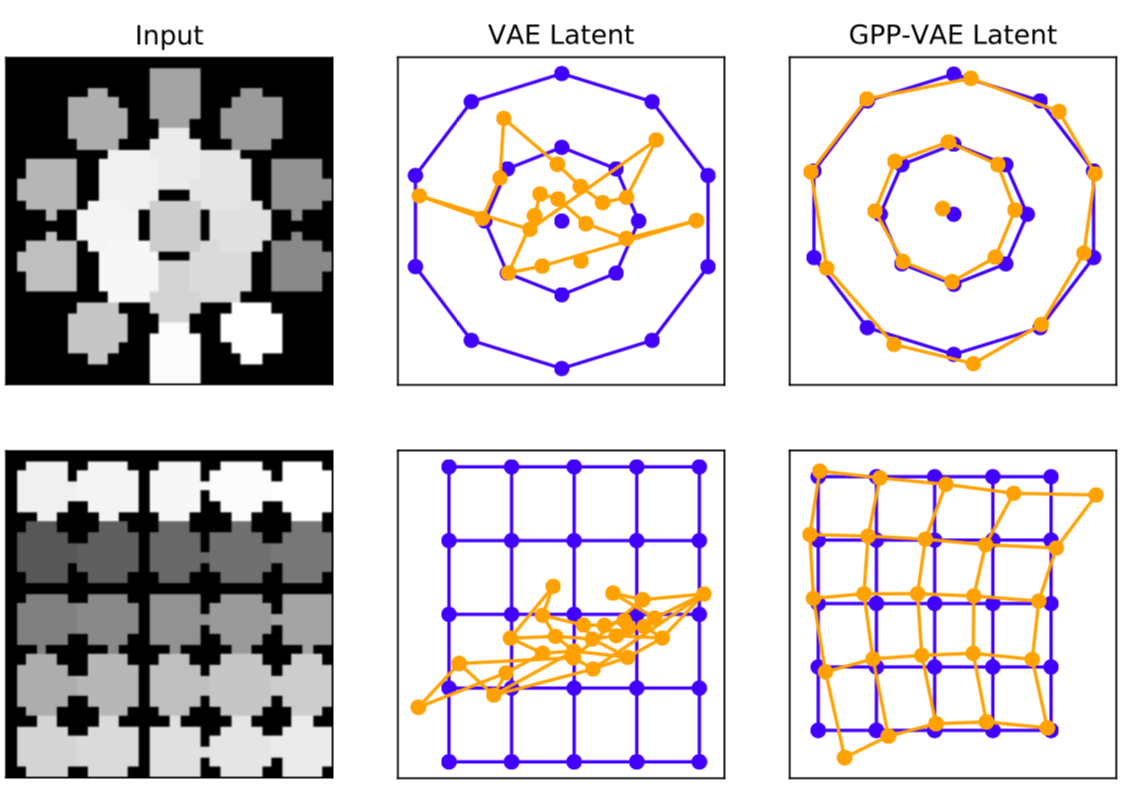
As a simple naive Baseline, we also trained a VAE without any correlation through time, the images are encoded in an i.i.d. fashion, as a result the latent space is rather messy and discontinuous, the top row is input video, middle row is VAE encoded latent \((x,y)\) and the bottom row is the GP-VAE encoded \((x,y)\)

If we consider a fixed pattern of images, and ask the encoder for an \((x,y)\) position in latent space, one would hope that a set of frames where the ball movies smoothly from one side of the screen to another would lead to a continuous set of latent points. However, this continuity from pixels to latents is not preserved by a standrard VAE, but is preserved by the GP-VAE. In the plots below, the lines are only there for visual clarity, we made a specific set of frames and plot the encoded \((\mu^*_x(v_t), \mu^*_y(v_t))\) points (above plots show \((\mu_x(t), \mu_y(t))\)).
Here we present some simple proof-of-concept results and, on this toy application at least, training is easy, yields an interpretable latent space that maps directly to pixel space. Next steps are to use the model on real data and reduce the cubic cost of GP inference for really long time series and evenetually augment an RL agent with the ability to predict physcially plausible latent states with uncertainty from visual input.
Feel free to play with the code and get in touch! scrambledpie@gmail.com