Continuous Multi-Task Bayesian Optimization with Correlation
Standard Bayesian optimisation deals with finding the best input \(x \in X\) to a stochastic noisy expensive black box function \(f(x)\). If I had, say, 10 expensive black box functions all over the same input domain \(f_{1}(x),..., f_{10}(x)\), surely I do not need to optimise all 10 independently?
We consider this problem and show that when given a range of objective functions (multiple tasks), optimizing one can speed up optimisation of the rest. Specifically collecting data (pick one \(f_{i}(x)\), pick one \(x \in X\), observe one \(y\)) accounting for how that new data point influences all functions can lead to significant performance improvement across all functions.
We propose the Regional expected Value of Improvement algorithm for this purpose and it looks like this:
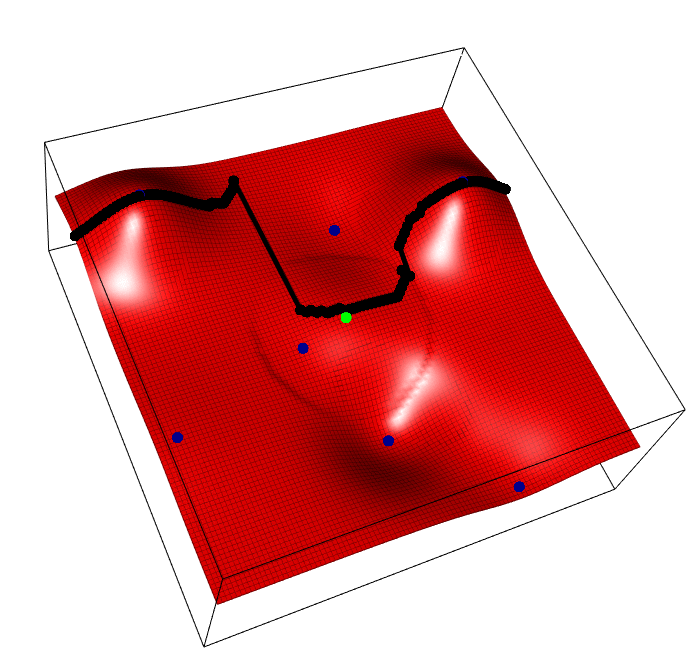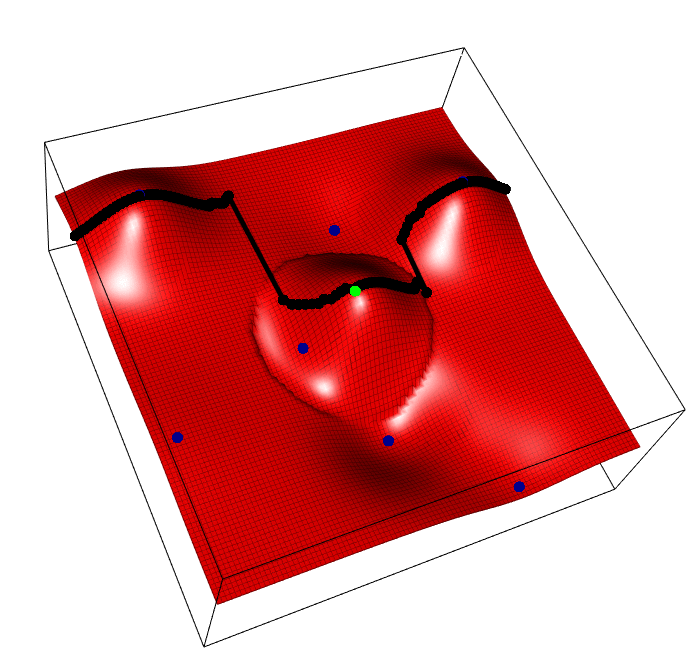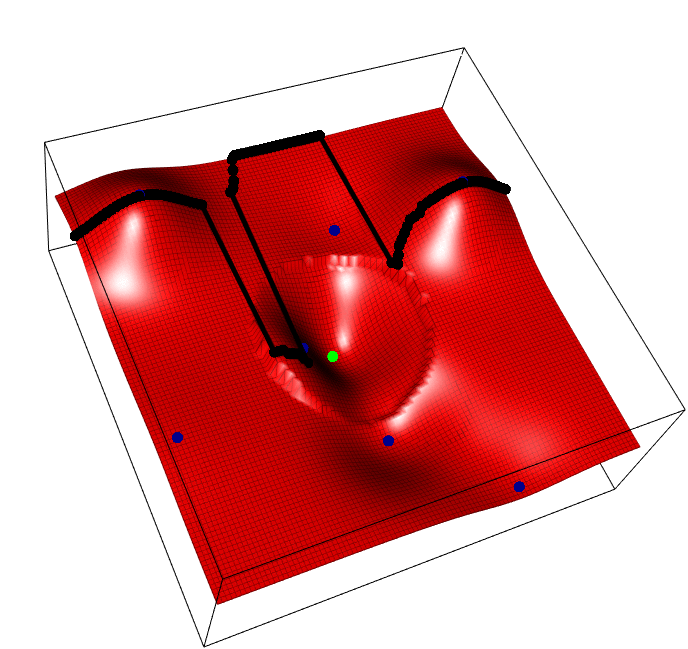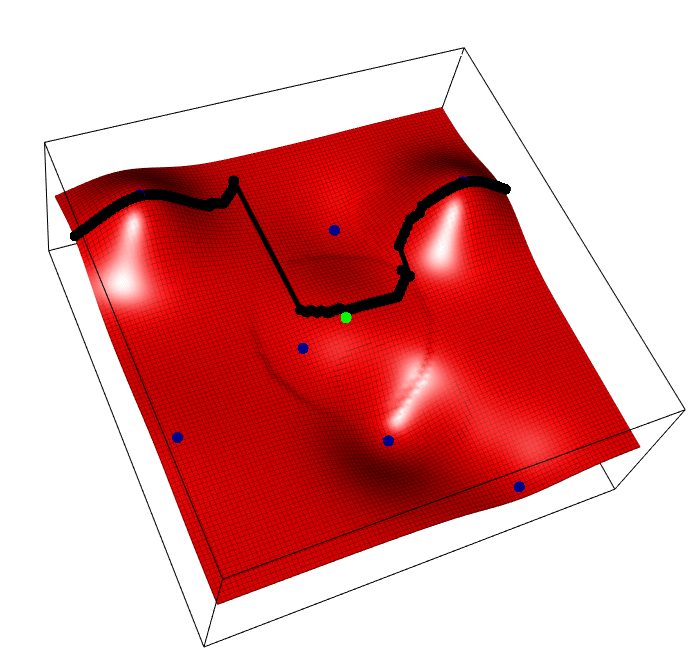
The horizontal axis is the task parameter \(i\), the depth/vertical axis the input for that task \(x\), and we aim to find the best input for each task \(max_x f(i,x)\), i.e. optimize each vertical slice. Blue points are observed points, the green point is one possible new point whose y value is random, and the black points show the predicted peak of each slice, that will change as a result of the new green addition.
The acquisition funciton, REVI, simply says, find the single green point that maximses the average height of all black points.